
Sheet1 and empty the cells not used by your model. The number of constants you used for the model. Please check whether the value in cell B2 is exactly one less than The cell will turn red for values over 0.05. So less is more for this cell, you want it to stayīelow 0.05. Less than 0.05, there is a 95% probability your model is correctlyįitting the data. On the ANOVA tab, you can find the ANalysis Of VAriance table, which Note that it also enables you to ask for a couple of Some time the "Solver Results" dialog opens, giving you some options on If you're happy with the current Solver settings, click Solve. So be prudent and critical on whether or not you have actually reached aīest fit, the Solver may come up with non-optimal results, depending on

You can save and load Solver settings using the A bit of experimenting may be needed forīest results. Note that depending on your model type you may have toĬhange the solver settings. Unused constant cells are empty by selecting them and hitting the del That are used by your model, otherwise the degrees of freedomĬalculation (on the ANOVA sheet) will be wrong. The "By Changing Variable cells" box must ONLY point to the cells Make sure the "Set Objective" box points to the cell that contains Ribbon as the "Data Analysis" button I showed before.Īfter you have ensured the model formula is correctly entered inĬolumn C and the calculations work, click the Solver button. This adds the Solver button in the same location on the Use the Add-insĭialog I showed at the top of this article and check the box next to
#CUBIC REGRESSION EXCEL INSTALL#
Using Solverįirst of all, you need to install the Solver add-in. It is this cell G11 that we try to minimize using the Solver add-in. As you can see, below that table the residual Sum of Squares is Resulting constants and where the Solver add-in also returns the This table is where you enter your first initial guesses for the The const range names point to a second table in the file: Using the table references that current Excel offers, I included someĭynamic range names that point to the data.Ĭolumn with y values Constants of the equation
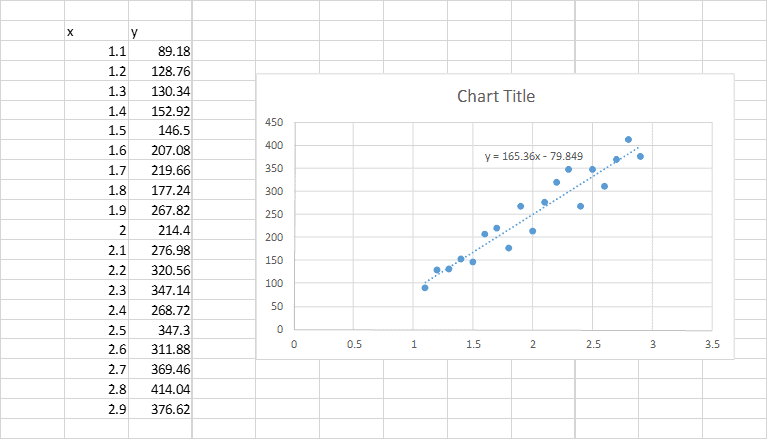
To ease working with the file I created some range names. The fourth column of the table is used to calculate the sum ofĪs you probably noted already, I used a couple of range names. =EXP(Const_a*xValues)*SIN(xValues)+Const_b Third column holds the formula that calculates the result of the fittedĮquation using the constants and the x-values. The most important area is the table starting in cell A1:Ĭolumn A holds your x-values and column B holds the y-values. The calculations and the data are concentrated on Sheet1 of the file. Least squares example How the file works Data Below you willįind a link to the file and an explanation on how the file is put I created an example file you can put to use directly.
Your x-es and to some cells for the constant(s)

"Regression" (without the quotes of course). To quickly access them, select an empty cell andĬlick shift+F3 to open the function wizard. There is a number of worksheet functions which you can also use to do This adds the "Data Analysis" button to your ribbon, on the Data tab,Īnalysis group (this is also the location where you can find the SolverĬlick that button to explore which regression tools are available. The add-ins list of Excel with the Analysis toolpak activated Office button, Excel Options, Add-ins tab, click Go): Regression tools in the Analysis Toolpak Add-inĪctivate the Analysis Toolpak in your list of Add-ins (File button or With some tricks you canĪlso perform LS on polynomes using Excel. Y=a.x+b, y-a.exp(b.x), y=a.x^b and etcetera. Fitting simple linear equationsĮxcel provides us with a couple of tools to perform Least SquaresĬalculations, but they are all centered around the simpler functions: Method here, just read up on the matter by clicking that link to Perhaps you did some measurements with results like this:Ī well known way to fit data to an equation is by using the If you're a properĮngineer, you also have some idea what type of equation should Way to fit your measurement results with a curve. Have probably done your bit of experimenting. If you're an engineer (like I used to be in a previous life), you Fitting curves to your data using least squares Introduction


 0 kommentar(er)
0 kommentar(er)
